 -clipping algorithm), where we assume that the
signal is a Gaussian with mean µi and standard-deviation
-clipping algorithm), where we assume that the
signal is a Gaussian with mean µi and standard-deviation
 i, or
lagi, 16-bit ~ N(µi,
i, or
lagi, 16-bit ~ N(µi,
 i2).
i2).
The lags computed by the spectrometer are 16-bit values. However, most pulsar observations do not need this much precision and can use 4- or even 2-bit values without significant loss of signal-to-noise. Therefore, the Spigot cards can truncate the lags to a lower precision before sending them to the acquisition computer. This enables faster sampling, more lags, and/or more IFs to be recorded while maintaining the same data rate.
To preserve signal-to-noise as much as possible when truncating the data, each individual lag has a scale and offset which are applied to it prior to truncation:
We first determine the statistics of the 16-bit signal robustly (using
an iterative  -clipping algorithm), where we assume that the
signal is a Gaussian with mean µi and standard-deviation
-clipping algorithm), where we assume that the
signal is a Gaussian with mean µi and standard-deviation
 i, or
lagi, 16-bit ~ N(µi,
i, or
lagi, 16-bit ~ N(µi,
 i2).
i2).
To measure how good the lower-precision representation is, we define an
error function
E(µi,
We plot results of simulations of degredation in
the Figures (below). With 16 bit data, the
finite precision (i.e. converting 2.5 to 2) has very little effect on
Ei as long as
The results, summarized in the Table (below), show that there is a
range of
To then have the least degredation when truncating our input signal,
we set Mi=-µi and i =
That there is a somewhat broad range for
In the discussion above, we assumed that the data could be
characterized properly. When operating in a 16-bit mode, this is
easily done, but at the same time it is not crucial to set the scales
and offsets precisely as a broad range of values will allow operation
with negligible degredation. For modes with < 16 bits, and especially
those with
 i (1/N)
i (1/N)  i (lagin - lagout)2.
We must scale this by 1/
i (lagin - lagout)2.
We must scale this by 1/ 2 for the results to be comparable.
Therefore, plotting E(µi,
2 for the results to be comparable.
Therefore, plotting E(µi, i)
/
i)
/  i2 vs. (µi,
i2 vs. (µi, i) should allow us to
determine the optimal range of (µi,
i) should allow us to
determine the optimal range of (µi, i) where the
degredation is minimized. Ei/
i) where the
degredation is minimized. Ei/ i2 is then
related to the more standard signal-to-distorion ratio (SDR) by
SDR
i2 is then
related to the more standard signal-to-distorion ratio (SDR) by
SDR  -10 log10 Ei \
-10 log10 Ei \  i2,
where SDR is in dB.
i2,
where SDR is in dB.
 i
i 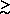 100. The largest effect is the
limited range of the data, which causes misrepresentations when
100. The largest effect is the
limited range of the data, which causes misrepresentations when
 i
i 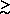 7000. The optimal range (for µi=0) is
100
7000. The optimal range (for µi=0) is
100 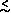
 i
i 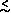 7000.
Changing µi has very little effect on
E(µi,
7000.
Changing µi has very little effect on
E(µi, i) as long as it is |µi|
i) as long as it is |µi|
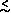 5000. Above
this, it begins to push data on one side of the Gaussian towards a
limit. The optimal region has Ei/
5000. Above
this, it begins to push data on one side of the Gaussian towards a
limit. The optimal region has Ei/ i2
i2
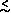 10-6. For
8-bits, this is similar to the 16-bit case, where the results are good
for 20
10-6. For
8-bits, this is similar to the 16-bit case, where the results are good
for 20 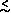
 i
i 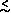 50
and |µi|
50
and |µi| 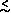 10, and the
optimal region has Ei/
10, and the
optimal region has Ei/ i2
i2 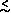 10-3.
With the 4-bit case the effects of truncation are becoming more apparent, as only
when 1.7
10-3.
With the 4-bit case the effects of truncation are becoming more apparent, as only
when 1.7 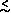
 i
i 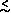 3 and
|µi|
3 and
|µi| 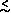 2 are the
results good. The optimal region has Ei/
2 are the
results good. The optimal region has Ei/ i2 ~
10-2 - 10-1. The 2-bit case has the smallest region with
acceptable degredation. For 0.6
i2 ~
10-2 - 10-1. The 2-bit case has the smallest region with
acceptable degredation. For 0.6 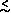
 i
i 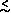 1,
results are good, but µi=0 is required. The optimal region
has Ei/
1,
results are good, but µi=0 is required. The optimal region
has Ei/ i2 ~ 0.8 - 1.0.
i2 ~ 0.8 - 1.0.
 i for which the lagout have acceptable deviation from
the lagin (µi=0 is the best value in all cases). The values of
i for which the lagout have acceptable deviation from
the lagin (µi=0 is the best value in all cases). The values of
 i that minimize Ei/
i that minimize Ei/ i2
give SDRs comparable to the best values obtainable (e.g. http://www.data-compression.com/vq.html).
i2
give SDRs comparable to the best values obtainable (e.g. http://www.data-compression.com/vq.html).
 opt/
opt/ i, where
i, where
 opt is the optimal value of
opt is the optimal value of  for a given
precision, listed in the Table. Prior to truncation the
signal will then be ~N(0,
for a given
precision, listed in the Table. Prior to truncation the
signal will then be ~N(0, opt2), as desired.
opt2), as desired.
 opt is
crucial, as we have assumed that the statistics of the incoming signal
are stationary. Strong, variable sources or interference can alter
the statistics. So we will normalize the signal for the middle of the
optimal range (perhaps slightly to the low side of that), and then
variations in signal strength will not significantly change the
quality of the data unless
opt is
crucial, as we have assumed that the statistics of the incoming signal
are stationary. Strong, variable sources or interference can alter
the statistics. So we will normalize the signal for the middle of the
optimal range (perhaps slightly to the low side of that), and then
variations in signal strength will not significantly change the
quality of the data unless 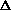
 ~
~  , which should
only happen if the antenna temperature T fluctuates by
, which should
only happen if the antenna temperature T fluctuates by 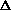 T ~ T.
This may happen due to significant RFI, but this will
generally wash out the data too so that it will not limit our
precision.
T ~ T.
This may happen due to significant RFI, but this will
generally wash out the data too so that it will not limit our
precision.
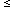 4 bits, the scales and offsets are more important,
but with some low-precision data it is hard to characterize it
(determine its mean and standard-deviation). Therefore, the spigot
computer can direct the spigot cards over the serial connection to
enter a temporary 16-bit mode. This mode is not meant for normal
operation and does not supply data for every time sample (if it did,
it would violate the 25 Mb/s constraint on the system). For example,
in mode 5 the data have 4-bits per lag, so the temporary 16-bit mode
only supplies data every fourth time sample. In this way the data
rate is held constant. While losing three out of four samples is not
useful for observing, it does not degrade the data in a statistical
sense, so these data can be used to determine the means and
standard-deviations of every lag. The appropriate scales and offsets
are then computed and sent over the serial connection, and finally the
spigot cards are directed to return to the normal 4-bit mode.
4 bits, the scales and offsets are more important,
but with some low-precision data it is hard to characterize it
(determine its mean and standard-deviation). Therefore, the spigot
computer can direct the spigot cards over the serial connection to
enter a temporary 16-bit mode. This mode is not meant for normal
operation and does not supply data for every time sample (if it did,
it would violate the 25 Mb/s constraint on the system). For example,
in mode 5 the data have 4-bits per lag, so the temporary 16-bit mode
only supplies data every fourth time sample. In this way the data
rate is held constant. While losing three out of four samples is not
useful for observing, it does not degrade the data in a statistical
sense, so these data can be used to determine the means and
standard-deviations of every lag. The appropriate scales and offsets
are then computed and sent over the serial connection, and finally the
spigot cards are directed to return to the normal 4-bit mode.
Optimal  i for reduced-precision Gaussians
i for reduced-precision Gaussians
Bits Range for  i
i
E(0,  i)/
i)/ i2
i2
2 0.6 - 1 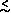 1
1
4 1.7 - 2.5 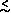 10-1
10-1
8 20 - 40 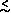 10-3
10-3
16 100 - 7000 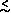 10-6
10-6
Error in estimating a Gaussian with 16-precision (right) and
8-bit precision (left). The solid curves and lower axes are for µi=0,
while the dashed curves and upper axes are for  i=6000
(16-bit) and
i=6000
(16-bit) and  i=33 (8-bit).
i=33 (8-bit).
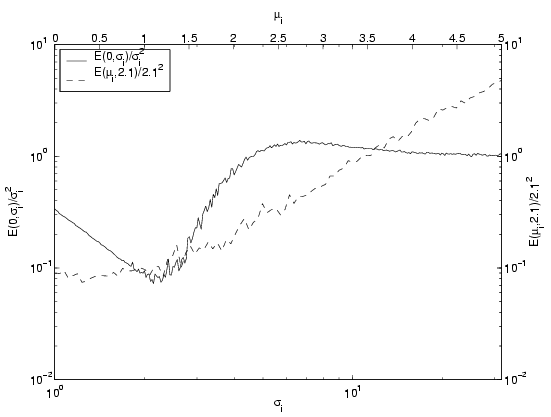

Error in estimating a Gaussian with 4-precision (right) and 2-bit
precision (left). The solid curves and lower axes are for µi=0,
while the dashed curves and upper axes are for  i=2.1
(4-bit) and
i=2.1
(4-bit) and  i=0.8 (2-bit).
i=0.8 (2-bit).