Class Outline
-
Brainstorming question:
-
Show overhead of typical galaxy, maybe within a cluster of galaxies.
-
Ask: "Suppose you are an astronomer who has just taken this image. As you
look at this object, what are the things you would like to know? Example
answers:
-
What is the object -- give them "galaxy" if they don't know
-
How big are galaxies?
-
How far away?
-
How are they grouped?
-
What are galaxies made of?
-
Why do they look the way they do?
-
Are galaxies moving? In what way?
-
How old are galaxies?
-
What is our galaxy like?
-
Explain that over the course of this workshop we'll be able to answer some
of these questions. To do so, we'll use spectral lines.
-
Exploring Optical Spectral
lines:
-
Use overhead projector, cardboard, and grating to display optical continuum
spectra.
-
Use light meter (if possible) to show that the intensity of light in spectra
varies from one color to another. Or, have them estimate the changes in
brightness.
-
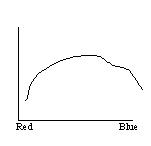
Graph the data implied by the light meter or as guessed by the eye. If time,
have students make the measurements and graph their result. [NOTE: most light
meters measure intensity on a base-2 logarithmic scale so you might have
to teach them how to do the converting to a linear scale] Graph should look
like:
-
Use glow tubes and slide-mounted gratings to display spectral lines of H,
Ne, Hg, flourescent lamp....
-
Use slide projector to show a slide of what they should be seeing with grating.
-
Use light meter (if possible) to measure how bright the spectral lines are
on the slide. NOTE: Since this is a photograph of a set of spectral lines,
the intensity you measure for the lines depends upon the color sensitivity
of the photographic film. Answers are only roughly correct.]
-
Graph the data implied by the light meter or as guessed by the eye. The graph
for, for example, Hg should look
like:
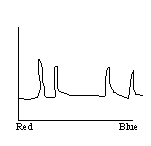
-
Can you tell what gases are in an object without having a sample of the
object?
-
Experiencing Doppler shifts:
-
Does anyone know what the Doppler effect is?
-
Use buzzer on string to demonstrate the Doppler effect for sound. NOTE: The
equations are the same for sound and light but you need a 'radar gun' to
demonstrate the Doppler effect for light waves.
-
Show viewgraph showing the Doppler effect. Explain red and blue shifts in
terms of 'lower' and 'higher' frequencies.
-
What kinds of motion could cause a shift in frequency of observed spectral
lines?
-
Whole object moving
-
Object might be rotating
-
All one sees is motion along the line of sight. If object is moving perpendicular
to the line of sight, no Doppler shift.
-
Exploring the radio spectral lines from atomic
H produced by galaxies:
-
Hand out ten images of galaxies and their corresponding H spectra.
-
Explain the axes of the spectra.
-
Explain how some spectra have different y-axes since there spectral line
are stronger than the rest.
-
Explain that all the images are 20 arcmin by 20 arcmin in size.
-
The NRAO 140-ft produced the H spectra
-
Anyone can download images of astronomical objects: http://skyview.gsfc.gov
-
Tell them the H gas is found between the stars as part of the Interstellar
Medium. 90% of the atoms in the ISM is H.
-
Explain that, when measured in the laboratory, H emits radio waves at 1420.4
MHz. Why aren't the galaxies emitting at 1420.4 MHz?
-
Have the students arrange the spectra (on the floor). [Work in teams?] Tell
them to use whatever scheme of classification they want. If they need hints,
tell them they can try the size of galaxy, magnitude of the Doppler shift,
tilt of galaxy, ...
-
They should note:
-
The smaller the galaxy image, the higher the Doppler shift. All are moving
away from us!!!
-
The smaller the image, the weaker the area under the spectral lines -- THUS:
the further the galaxy is away from us, the dimmer the (spectral-line) light
we receive.
-
The smaller the image, the further the galaxy is away from us -- THUS: The
higher the redshift, the further the galaxy is away from
us.

-
The more the galaxy is tilted, the wider the spectral lines and the more
'double-peaked' -- THUS: The more the galaxy is tilted, the more we can see
its rotation velocity. Half of the galaxy is coming towards us, the other
away from us.
-
Explain the terms 'face-on' and edge-on' galaxy.
-
Show viewgraph on how to find the distance of galaxy from its velocity. Have
the student groups pick a galaxy and find its distance. Use "Useful Equations"
viewgraph to give formulae.
-
Weighing a galaxy
-
Have each group pick a spectra from a 'tilted' galaxy and that from a 'face-on'
galaxy.
-
Viewgraph of Gravitational Force = Centripetal Force. If you know the size
of a galaxy and how fast it is rotating, then you can calculate its mass!!
-
If you want, go over derivation of centripetal force
-
Then, explanation of gravitational force
-
Viewgraph of how to find the size of a galaxy. Hand out size rulers. Have
the groups calculate the size of their galaxies.
-
Viewgraph of how to find the rotational velocity of a galaxy. Hand out 'width'
rulers. Have them measure the rotational velocity of their galaxies.
-
Have each group calculate the mass of their 'tilted' galaxy. Compare results
(they should all be, within a factor of ten, about the same). Give 'example'
calculation viewgraph if running out of time.
-
Viewgraph of the correction factor. Can you use this method to find the mass
of their face-on galaxies? No!!! No rotational motion along the line of sight!!
What can we do with the 'face-on' galaxies?
-
How much gas in a galaxy
-
Hold up one, then two, then three flashlight. If you only saw the light from
the flashlights, how could you calculate the number of flashlights I was
holding? You need to know the light given off by a single flashlight and
my distance.
-
If you knew the light given off by the H in a galaxy, and you knew the amount
of light given off by a H atom in the lab, could you calculate the number
of H atoms in a galaxy? Yes!!!
-
Viewgraph of amount of gas in a galaxy. Hand out 'grids'. Have groups calculate
the H mass of both their galaxies. They'll need the distances they measured
above. Should be a few percent of the total mass and all about the same value
(to within a factor of ten).
-
How hot is the H gas in a
galaxy?
-
What could be cause of the width of the lines for the 'face-on' galaxies?
Brownian motion (maybe)?
-
Viewgraph of temperature calculation. Have them calculate T and compare answers.
Are these T reasonable? No..... Too hot!!! What else could the widths be,
then? Astronomers still don't know the true answer to that one!!


