Tests of rms vs integration time: K-band

Report on tests performed January 7-8, 2004 with 800 MHz bandwidth.

Summary

Procedure

We used the GBT spectrometer in 800 MHz mode with 2048 channels per spectrum (channel spacing 391 kHz). Two spectral windows were used, centered at 24.0 and 24.8 GHz. Both beams were used and "nodding" observations were done, alternately putting the source in beam 1 and beam 2. We did not do beam switching. Temperature calibration was done by injection of a noise cal signal at 1 Hz.

A "dummy" celestial position was tracked: RA=14:00 hours, DEC=25 degrees. The telescope elevation was about 50 degrees. Each nodding pair consisted of two minutes integration, i.e., a total of 4 minutes on-source integration time for each pair. Thirty nodding pairs were done, for a total of two hours integration time.

The nodding scans were reduced using Jim Braatz's "reduce.g" program. The "reduce" program converted temperature to flux density assuming an aperture efficiency of 0.55 and an atmospheric tau = 0.05.

The configuration file used to set up the observation may be seen here.

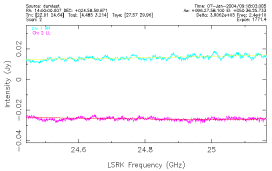
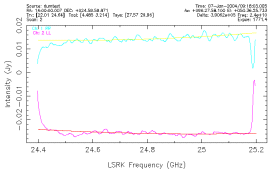
A typical reduced spectrum from one nodding pair is shown in the following plot.

In this plot the smooth lines are the 2nd-order polynomial baselines that were fit, omitting channels near the edges of the spectrum. After subtracting the baseline, the rms flux density was calculated.

In this way the rms was calculated for a single nodding pair, for the average of two pairs, 4 pairs, and so forth. As a final step, the data from all scans were averaged together and the spectra at the two frequencies were averaged to give 4 hours of effective integration time.

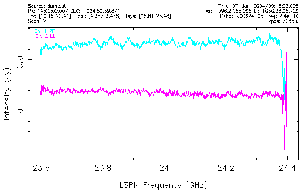
This final averaged spectrum (equivalent to 4 hours effective integration time) is shown in the next plot.

Effect of integrating

Tabulation of the RMS for different integration times is shown in the following table. The "calculated" column gives the prediction of the radiometer equation for Tsys = 30 K. The weather was excellent for this run, with Tsys in the 25-35 K range.
Integration Time rms in 24.0 GHz band rms in 24.8 GHz band Calculated rms
(minutes) RCP (mJy) LCP (mJy) RCP (mJy) LCP (mJy) (mJy)
4 4.63 2.82 3.89 3.00 1.73
8 2.01 2.00 2.94 2.73 1.22
16 1.34 1.92 2.18 1.79 0.86
32 0.95 0.97 1.40 1.15 0.61
60 0.76 0.72 1.07 0.99 0.45
120 0.59 0.47 0.81 0.61 0.32
240 0.50 0.34 0.22
Note: the radiometer equation for this case is as follows:
  • Srms = (K1 * Tsys / G) / sqrt( K2 * Teff * bw)
  • where K1=1.235, G=1.5 K/Jy, K2=2, Teff is integration time in seconds, and bw =(800E+6 Hz/2048)

    These data are plotted in the following graph.

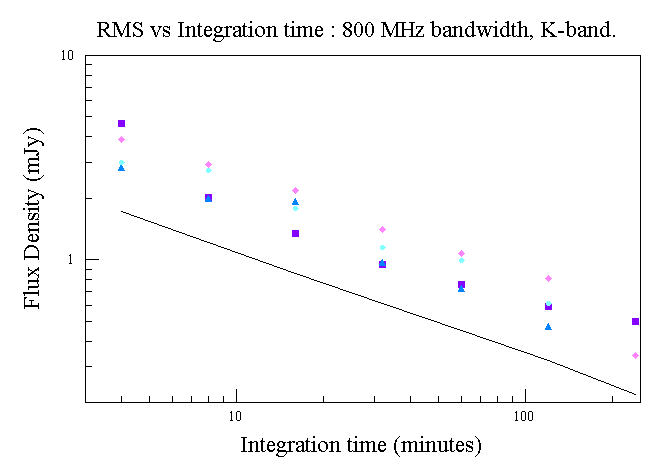
    One may note that the measured RMS is decreasing with total integration time as expected, but that the values are about two times what is predicted by the radiometer equation. The plots show small ripples of with width of about 50 MHz. The size of these ripples seems to be decreasing with integration time.

    Effect of smoothing

    One may also ask whether smooting the spectra to lower resolution will increase the sensitivity. To test this, we took a 60-minute integration and did a Gaussian smoothing over 4 channels and over 16 channels, decreasing the resolution by a factor of 4 and 16 respectively. The unsmoothed spectrum is shown in the next graph.

    The spectrum after 16-channel smoothing is shown here.

    The rms values after subtracting a 2nd order polynomial and avoiding the end regions of the spectra are tabulated in the following table:
    #channels Smoothing RCP (mJy) LCP (mJy)
    1 1.04 0.87
    4 0.95 0.71
    16 0.84 0.58
    While one might expect the rms to drop by a factor of 4 when using a 16-channel smoothing, we find that the actual drop is 20-30 %. Apparently there is a systematic ripple that prevents reaching expected noise levels. The typcial width of the ripples is about 80 channels (20 MHz), so the ripple is not diminished by a smoothing length less than this.